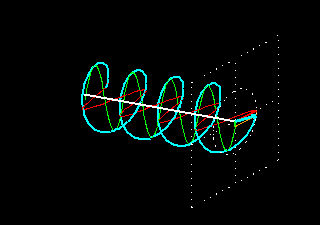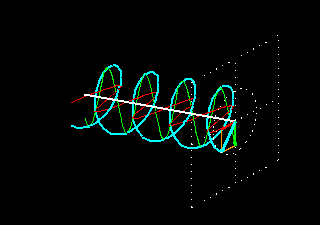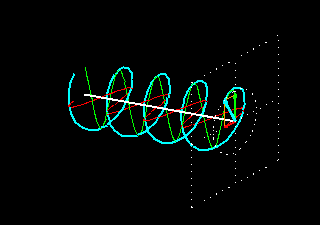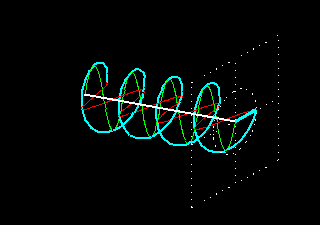
When two waves plane-polarized in two perpendicular planes meet out of phase then the wave resulting from the superposition of the two waves will no longer be plane-polarized.
The following animation presents the superposition of two waves that have the same amplitude and wavelength and are polarized in two perpendicular planes but there is a phase difference of 90 degrees between them. A phase difference of 90° means that when one wave is at its peak then the other one is just crossing the zero line. The superposing components are visualized with red and green colors and the wave resulting from the superposition is shown in light blue.

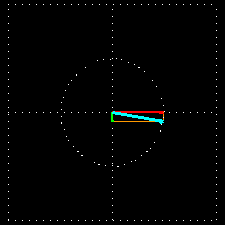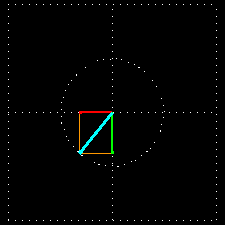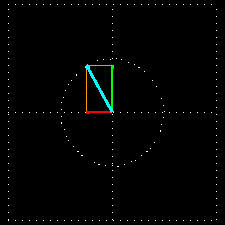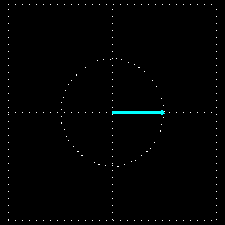
When the intersecting plane is looked at from the front then the following image is seen:
(Attention! The two animations are not synchronized!)
The result of the superposition is a special electromagnetic wave. At any fixed point in space that is in the line of the propagation of this wave, the electric field vector rotates in a circle while its length remains constant. Such waves are called circularly polarized waves. As the 3D picture shows, a circularly polarized wave can be visualized with a spiral line; the wave propagates as a function describing a spiral instead of one describing a sinus curve.
In this picture, the electric field vector rotates clockwise when looked at from the direction of propagation.