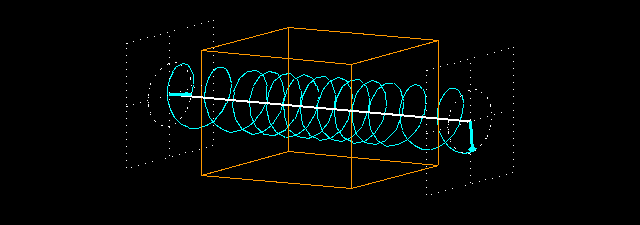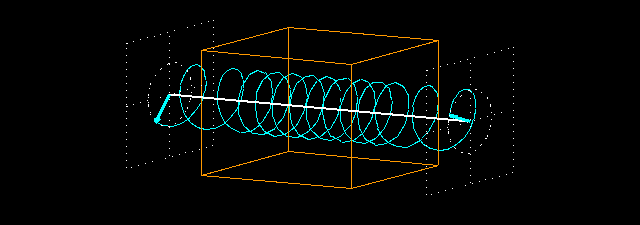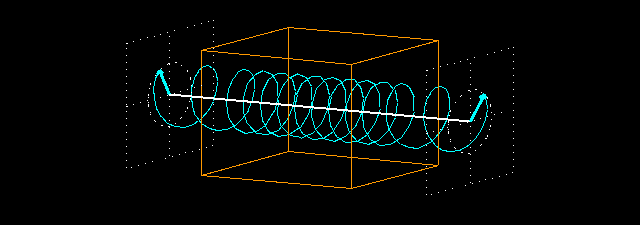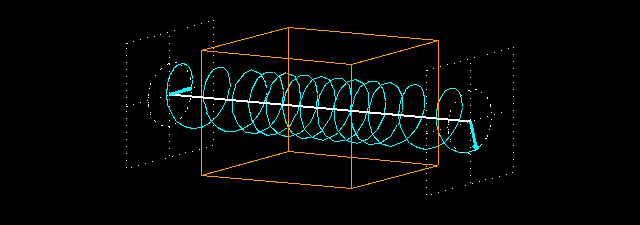
What happens when a circularly polarized wave traverses a non-absorbing medium with a refraction index > 1.0 (n = 2.2). We measure the field vector before and after the piece of material.

The following animation shows the two intersecting planes from the front. On the left, before the material, on the right, after the material.
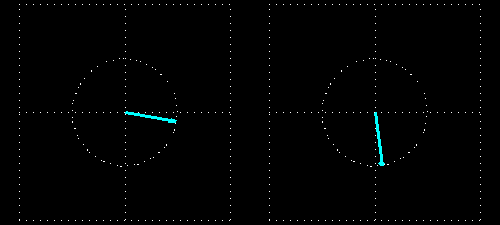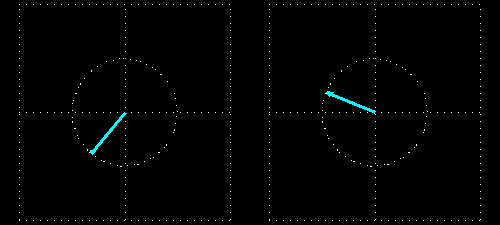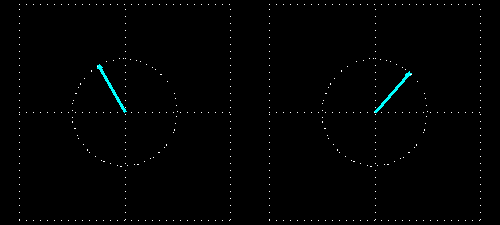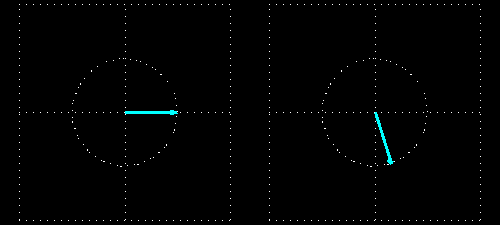
The wavelength is much smaller in the medium than before and after it because the light is slower in the medium. The intensity of the light does not decrease: the field vector of the exiting light is of the same length as that of the entering light because there is no absorption.
But the phase of the wave changes here again. If the piece of material was not present then the field vectors at the two intersecting planes would rotate exactly in the same phase because their distance is an integral multiple of the wavelength. This situation changes when we put the piece of material in between the two intersecting planes: the light slows down in the piece of material (whose thickness is 4 times the wavelength), and it makes 8.8 (4 x 2.2) full periods inside the material instead of 4 full periods. This results in a 72° phase difference between the entering and exiting light waves. This is clearly seen in the animations showing the intersecting planes.
What happens when the light wave traverses a medium that absorbs AND refracts the light at the same time - the amplitude decreases and phase changes of the light exiting the material in comparison with the amplitude and phase of the light entering the material.