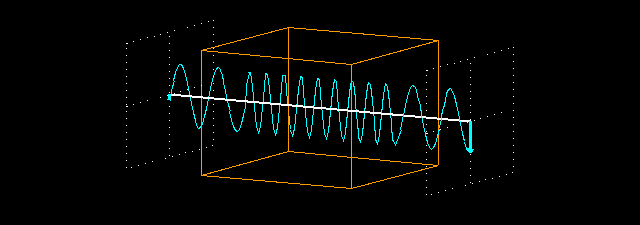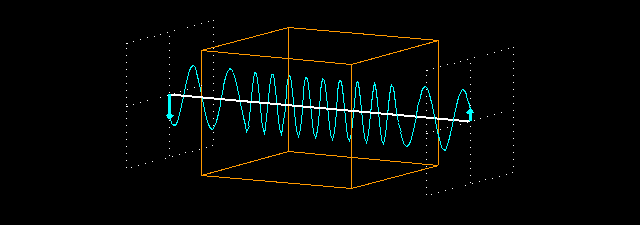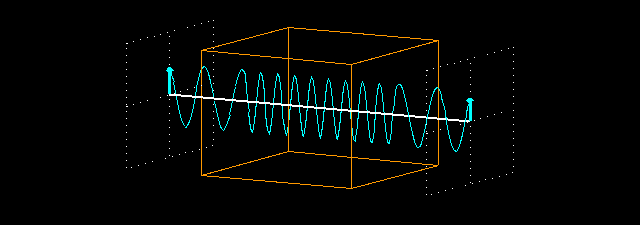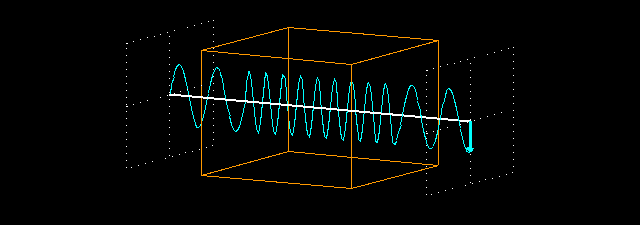
Animation: what happens when a plane-polarized wave traverses a non-absorbing medium with a refraction index > 1.0 (n = 2.2). We measure the field vector of the light wave before its entry into the medium and after its exit, just like on the previous page.

The following animation shows the two intersecting planes from the front. On the left, the field vector before the light enters the material; on the right, after the light exits the material.
When the light beam enters the piece of material, it slows down because the refracting index of the material is greater than 1.0. Its frequency does not change, therefore its wavelength decreases (the product of the frequency and the wavelength should be equal to the velocity of light). In these animations, we used a refraction index n=2.2. This means that the velocity of light in the medium is 1/2.2 times the velocity of light in vacuum, and its wavelength also decreases to 1/2.2 times the original value. When the light exits the material, its velocity and wavelength are restored to their original (vacuum) values. Since the material does not absorb light, the intensity of the light does not decrease.
The distance between the intersecting planes in front of and behind the piece of material is exactly 8 times the vacuum wavelength of the light. Therefore, if the piece of material is not present, the field vectors at the two intersecting planes oscillate in exactly the same way: they are in phase. But if the piece of material is placed between the two intersecting planes, the light slows down in the material and it has 8.8 full periods inside the material, instead of 4 periods. So there are 12.8 periods between the two intersecting planes (there are 2 periods before the piece of material and 2 periods after it). Because this is not an integral number, the two field vectors at the intersecting planes do not oscillate in the same phase any longer.