|
|
Roll mouse
over links at left to view static images below of different acetic acid titration
plots, or click on the links to open dynamic popup
charts.
|
|
Acetic
Acid Titration Equilibrium Reactions:
 Top Top |
|
1-Step Dissociation Reaction
desaturation, ionization |
 |
In the
one-step dissociation
(or ionization or
desaturation) reaction,
protonated or saturated acetic acid
releases an H+
(hydronium) ion converting into deprotonated or
desaturated acetate ion. |
 |
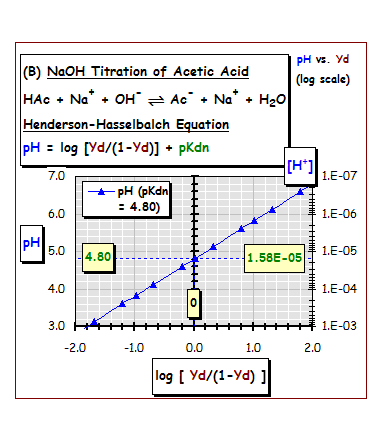
The
"dissociation fraction" (Yd) of dissociated acetic acid at equilibrium is
proportional to the equilibrium H+ concentration, [H+], and acetic acid's dissociation equilibrium constant
(Kdn). | |
|
1-Step Association
Reaction
saturation,
protonation |
 |
In the
one-step association (or
protonation
or saturation)
reaction, deprotonated or desaturated
acetate ion binds an H+
(hydronium) ion converting into protonated or
saturated acetic acid. |
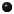 |
The
"association fraction" or
saturation fraction (Ya) of associated acetic acid at equilibrium is
proportional to the equilibrium H+ concentration, [H+], and acetic acid's
association equilibrium constant (Kan). | |
|
|
Key Chemical and Mathematical Formulation:
 Top Top |
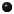 |
[
CH3COOH] = [HAc] = acetic acid equilibrium
concentration |
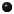 |
[
CH3COO-] = [Ac-] =
acetate equilibrium concentration |
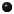 |
Co
= [Ac- ] + [ HAc ] = the total
equilibrium concentrations of acetic acid plus acetate. |
 |
Yd = the "dissociated
fraction," the total fraction of all molecules in
solution that are ionized or deprotonated. |
 |
Ya = the
"associated " or "saturated
fraction," the total fraction
of all molecules in solution that are protonated acetic acid
molecules. |
 |
Yd + Ya =
1: The fractions
of all molecules have to add up to
one. | |
Key Quantitative Relationships
Derived from the Equation for the Equilibrium Dissociation Constant,
Kdn
 Top Top |
 |
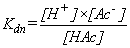 |
Note: pKdn =
-log(Kdn); Kdn =
10-pKdn
pH =
-log[H+]; & [H+] = 10-pH |
|
Recommended Exercises:  Top Top |
| 1. |
Prove
that Kdn = [H+]50%, where [H+]50% = the H+ concentration at
50% saturation.
Hint: Determine
[H+] at
Ya = 0.5 or Yd = 0.5 (i.e., at "50%
saturation"). | |
| 2. |
Prove that
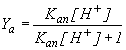 where where 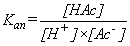 | |
| 3. |
Prove that
Kan = 1/[H+]50%, where [H+]50% = H+
concentration at 50% saturation.
Hint:
Determine [H+] at Ya = 0.5
or Yd = 0.5 (i.e., at "50%
saturation"). | |
|
|


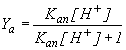 where
where